Ejemplo 21 de la sección 5.1.2, SISTEMAS RESORTE/MASA: MOVIMIENTO LIBRE AMORTIGUADO del libro Ecuaciones diferenciales con aplicaciones de modelado, de Zill, editorial CENGAGE Learning.

Una masa que pesa 4 libras se une a un resorte cuya constante es 2 lb/pie. El medio ofrece una fuerza de amortiguamiento que es numéricamente igual a la velocidad instantánea. La masa se libera desde un punto situado 1 pie arriba de la posición de equilibrio con una velocidad descendente de 8 pies/s. Determine el tiempo en el que la masa pasa por la posición de equilibrio. Encuentre el tiempo en el que la masa alcanza su desplazamiento extremo desde la posición de equilibrio. ¿Cuál es la posición de la masa en este instante?

Los siguientes comandos (uno por línea) representan el código utilizado en Matlab.

clc
% Se define t, desde t0=0.2 hasta t1=4, con incrementos Dt=0.01
t=0.2:0.01:4;
hold on;
% Definiendo la funcion
y = -exp(-4*t)+4*t.*exp(-4*t);
% Graficando la función
plot(t,y,’-.b’,’linewidth’,2);
title (‘Gráfica ecuación movimiento’);
xlabel(‘t, tiempo [seg],’);
ylabel(‘x(t), desplazamiento [pies]’);
grid on
hold off

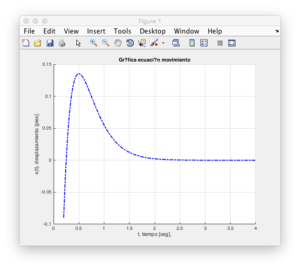
Obteniéndose la siguiente gráfica, donde se observa el comportamiento  de la ecuación de movimiento.

¡Saludos!

PD. Al copiar directamente el código al matlab, es necesario cambiar el apóstrofe para que lo reconozca adecuadamente.

PD.2. Es necesario utilizar el operador .* para realizar la multiplicación adecuadamente. (y no en términos de matrices)